Такой механизм позволяет объяснить также и причину расширение пространства между гравитационно связанными областями и его отсутствие внутри этих областей. Внутри гравитационно связанных областей, по всей видимости, "фоновой" области Материи труднее сформировать дополнительные атомы пространства. Здесь Материя, с одной стороны, исчерпала свой исходный материал, а, с другой стороны, сильное гравитационное поле просто противодействует появлению новых атомов.
Для большей наглядности проведем анализ формально с использованием аллегории железнодорожных путей со шпалами. Пусть расстояние между двумя объектами измеряется количеством шпал между ними. Примем, что исходное расстояние при t = 0 составляет одну шпалу r0 = 1.
Пусть удлинение, расширение пространства происходит монотонно таким образом, что его длина увеличивается за счет удвоения каждой шпалы в единицу времени. Здесь мы введем величину, которую назовём коэффициентом пространственного расширения (чтобы не путать его с масштабным фактором), равную в данном случае 2. Поэтому в следующий момент времени шпал будет уже две: ...
14.3.2. Интегральный закон Хаббла
Несложно показать, что при использовании изменяющегося во времени параметра eH(t) мы получим интегральное уравнение движения а(t) или r(t).
Для этого все одинаковые интервалы времени записываем количественно, а не в порядковом виде. Каждое следующее состояние пространства является расширением предыдущего интервала, уже испытавшего соответствующее расширение.
Отмечаем, что все интервалы времени Δti равны друг другу, а Hi – это значение параметра Хаббла, соответствующее текущему моменту времени этого i-го интервала. Для визуализации будем в уравнениях предыдущий интервал отделять от следующего закрывающей скобкой. Чтобы избежать "размножения" сопутствующих им открывающих скобок, мы их просто опустим, помня, что их может быть столько же, сколько и закрывающих: ...
... Выше такое же решение мы нашли для закона Хаббла с масштабным фактором (14.5) и (14.6). Уравнение описывает, как со временем увеличивается расстояние между двумя областями, находящимися в исходном состоянии на некотором расстоянии r0. Выше мы умышленно использовали константу в виде eH, чтобы получить именно такую запись (14.8), причем величина H окажется в точности равной постоянной Хаббла.
В заключение покажем, как с помощью этих уравнений производится построение диаграмм движения на примере условной галактики, сверхновой, находившейся в начале расширения пространства на удалении от Земли в 3 млрд. световых лет. Для наглядности рассмотрим условную Вселенную, расширяющуюся с параметром Хаббла H(t), имеющим множество изломов: участков убывания и возрастания. ...
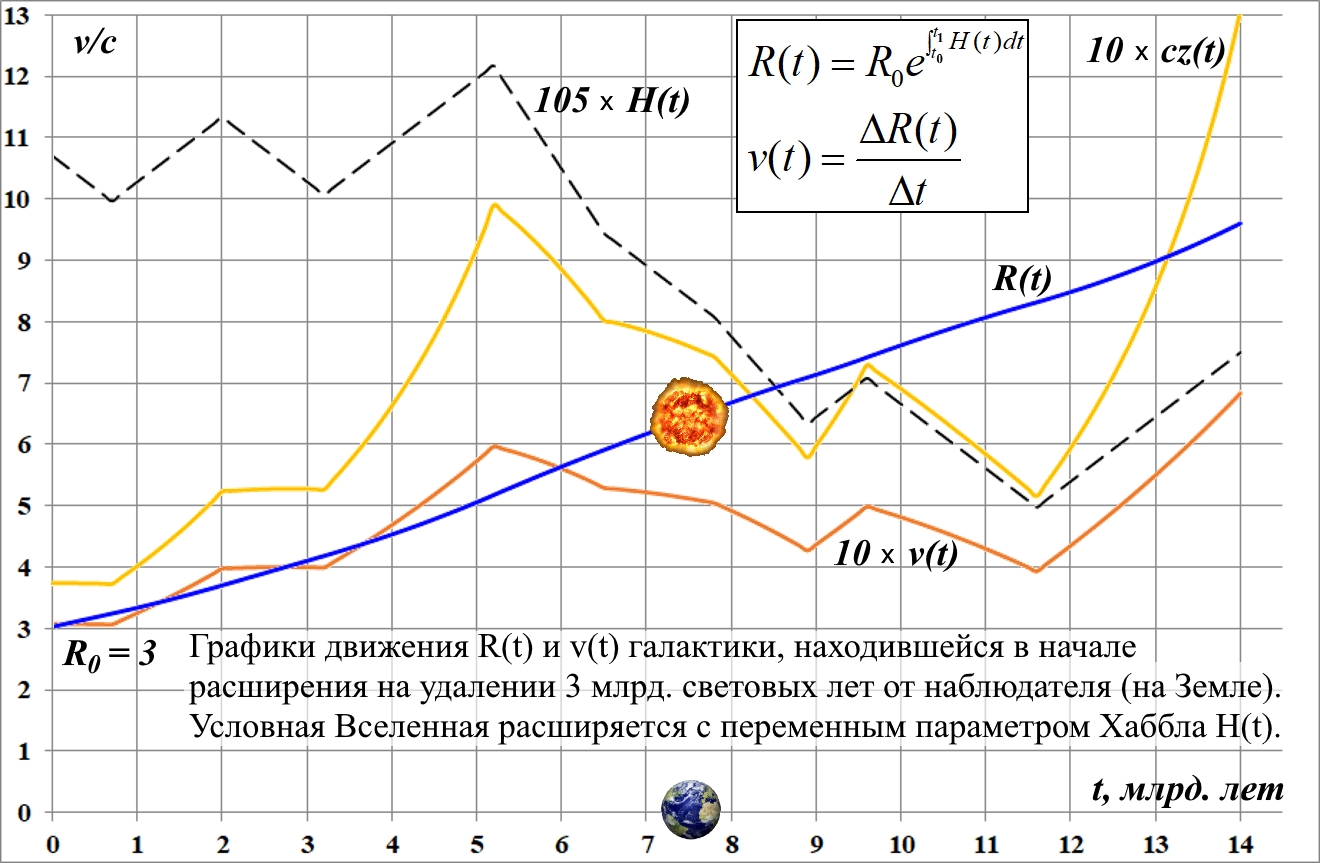
Рис.14.1. Пример диаграмм движения для переменного H(t)
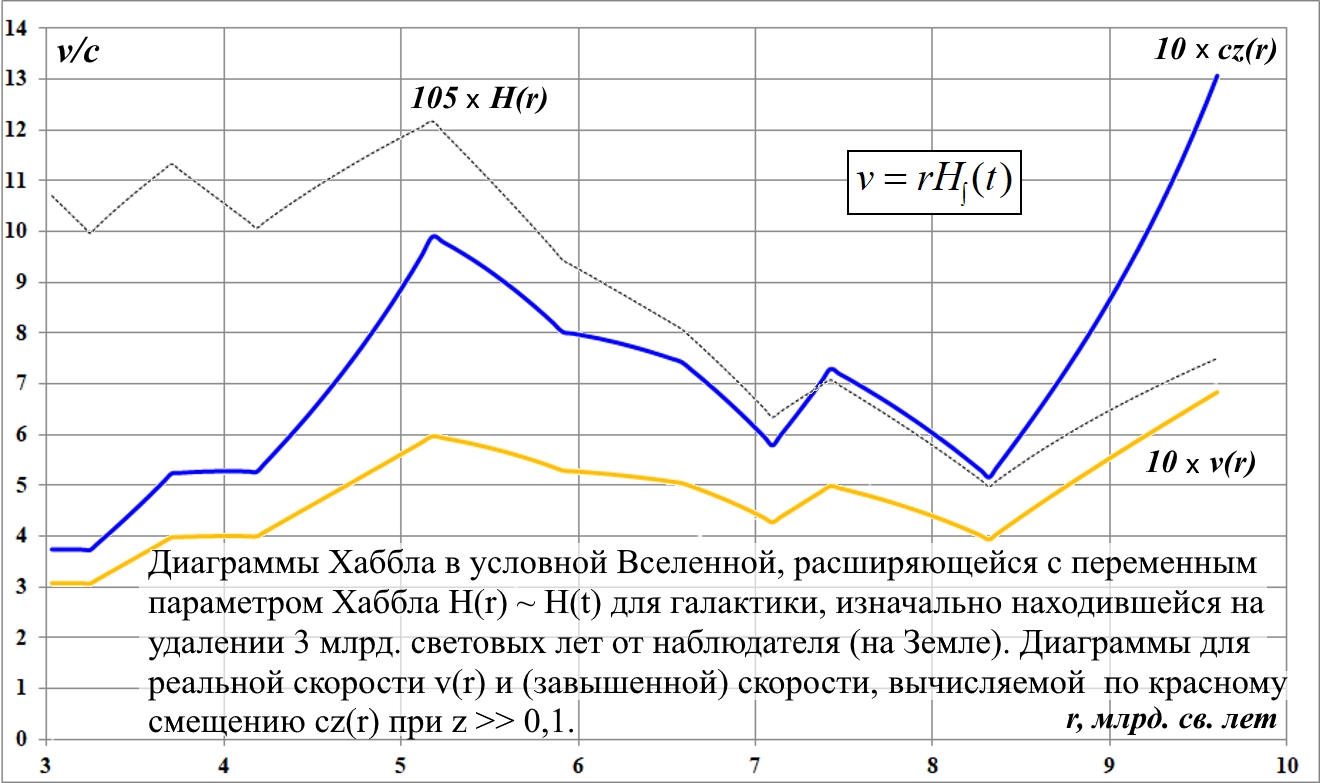
... Рис.14.2. Диаграммы Хаббла для v(r) и cz(r) во Вселенной с параметром Хаббла H(r)
